[데이터분석이론] #1 Missing data Mechanism

오늘은 통계학과 석사 첫학기 수업에서 배운 ‘결측자료분석’의 missing data mechanism 이론에 대해 다뤄보려고 합니다. 데이터분석에서 missing을 다루는 것은 매우 중요한 작업입니다. Missing data를 어떻게 다루느냐에 따라 model의 performance가 달라질 수 있기 때문입니다. Missing data를 처리하는 방법은 아주 다양한데, 다양한 imputation 방법을 적용하는 연습을 하기 전, 기본적인 missing data mechanism에 대해 설명하고 공부해보려고 합니다. (포스팅에서 다루는 내용은 모두 고려대학교 통계학과 송주원 교수님의 강의를 참고한 것입니다.)

1. Missing data mechanism 이란?

Missing data mechanism은 어떤 매커니즘이 결측을 발생시키는 지를 나타내는 것으로, missing data를 포함한 자료행렬(Y)와 missing이 어디서 발생했는지를 나타내는 무응답지시행렬(M)을 사용합니다. Missing data mechanism에는 다음과 같은 세 종류가 있습니다.

• MCAR(Missing Completely at Random): missing 발생 확률은 관찰(observed)여부에 상관없이 동일하다는 가정
• MAR(Missing at Random): missing 발생 확률은 관찰된 자료(observed data)에 의존한다는 가정. 즉, missing 이 발생한 자료에 의존하지 않음
• MNAR(Missing Not at Random): missing 발생 확률이 missing 발생한 자료에 의존한다는 가정
  
  이론상으로는 이 세가지 매커니즘의 차이가 무엇인지 잘 와닿지 않습니다. 그래서 간단한 샘플 데이터를 이용하여 세 매커니즘의 차이를 살펴보겠습니다. 코드는 R을 사용해서 작성했으며, 코드가 궁금하시면 다음 링크에서 볼 수 있습니다.
  R code link: https://github.com/hyewonleess/github_blog_posts/tree/main/missing_data

2. MCAR(Missing Completely at Random)

MCAR은 자료에서 missing 발생 확률이 자료의 관찰 여부와 상관없이 동일하다는 가정입니다. 즉, MCAR에서는 missing이 complete random으로 발생한다고 가정하는 것이죠! 더 쉽게 말하자면, 어떤 자료가 있을 때, 그 자료의 missing data는 일정한 패턴 및 규칙 없이 랜덤하게 발생했다면 이 자료는 MCAR 매커니즘을 만족시킨다고 볼 수 있겠습니다. 그리고 이제부터 관찰된 자료만 모아놓은 set을 complete set, missing 자료만 모아놓은 set을 incomplete set으로 명명하겠습니다.

예시 데이터셋은 다음과 같이 생성했다. z1, z2, z3는 표준정규분포를 따르는 500개의 데이터이다. 그리고 이 데이터를 이용해서 y1과 y2라는 변수를 생성했습니다.

z1 = rnorm(500,0,1)
z2 = rnorm(500,0,1)
z3 = rnorm(500,0,1)
y1 = 1+z1; y2 = 5+2*z1+z2

Missing은 y2 변수에서 발생하겠습니다. 이 때, missing을 발생하는 기준으로 잠재변수 u를 활용합니다. u<0 이면 y2를 missing으로 합니다. 즉, missing 발생확률은 약 50%라고 볼 수 있습니다.

u = a*(y1-1)+b*(y2-5)+z3

생성한 sample data가 어떤 구조를 가지는지 간단히 시각화를 하면 다음과 같습니다.

MCAR 가정을 만족시킬 잠재변수 u는 a=0, b=0을 대입해서 얻을 수 있습니다.

(1) Complete vs Incomplete set

이렇게 missing을 발생시켰는데, missing data의 분포가 어떻게 되는지 그래프를 통해 확인합니다. 빨간색으로 표시된 점이 바로 missing data인데, missing이 전체적으로 골고루 퍼져있기 때문에 MCAR가정에 맞게 missing이 랜덤발생했다는 것을 알 수 있습니다.
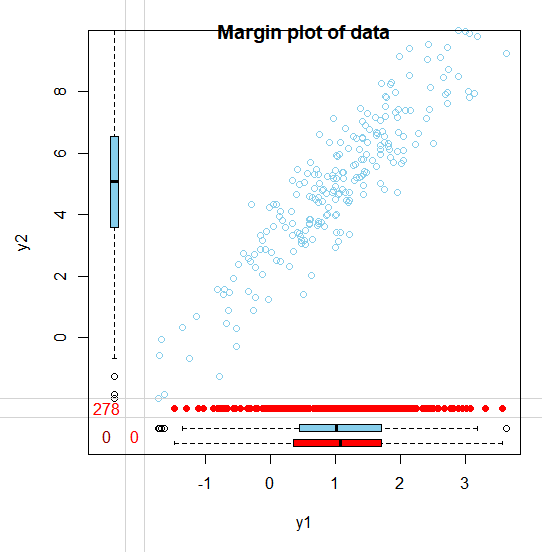
MCAR 가정 하에서 complete set과 incomplete set은 original data의 random sample이기 때문에 아래 그래프와 같이 각 set의 분포에는 별 차이가 없습니다.

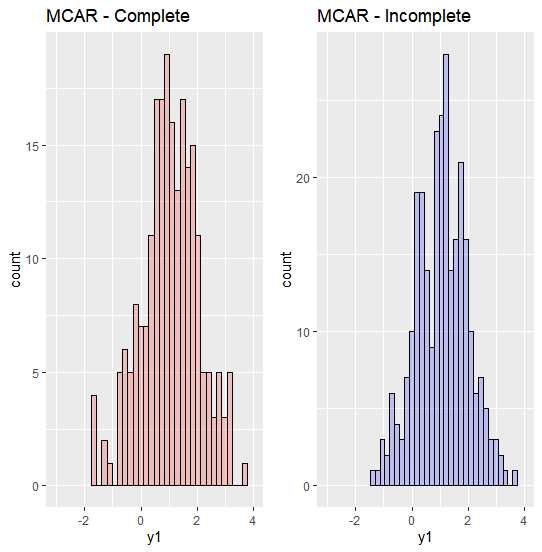
(2) Original vs Complete set - comparing distribution, mean, variance, regression coefficients

이번에는 원본 original data와 complete data의 분포와 각 set의 평균을 비교해보겠습니다. 이론적으로, MCAR 매커니즘에서는 original dataset과 complete dataset의 mean bias는 0 입니다. 그래프를 통해 다음과 같은 해석을 얻을 수 있습니다.

Interpretation

• MCAR 가정 하에서 original data와 complete data의 분포는 거의 차이를 보이지 않는다.
• MCAR 가정 하에서 original data의 mean과 complete data의 mean은 거의 차이를 보이지 않는다. 즉, MCAR 가정 하에서 mean bias는 0에 가깝다.
• original data와 complete data의 분포가 비슷하기 때문에 variance도 비슷한 것을 예상할 수 있다.
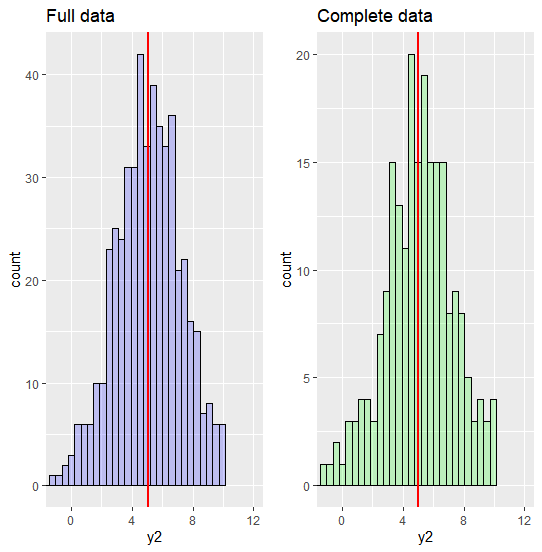
  이 해석이 맞는지 R코드 결과를 통해 확인해보겠습니다. Original data의 mean은 5.011, variance는 4.66 이고 complete data의 mean은 5.029, variance는 4.715 인데, 실제로 mean과 variance에서 bias는 거의 발생하지 않았다고 할 수 있습니다. (이론적으로는 bias가 0이 되어야 하나, sample data의 크기가 500으로 다소 작기 때문에 이정도의 오차는 발생할 수 있습니다.)
  
  

  회귀계수 비교

  두 set의 regression coefficient(회귀계수)를 비교해도 비슷한 결과가 나옵니다. 아래 그래프에서 파란색 회귀선은 original data에서, 빨간색 회귀선은 complete data에서 구한 것입니다. MCAR 가정 하에서 두 회귀계수도 거의 일치한다는 것을 알 수 있습니다. 이론적으로 회귀계수의 complete case 추정치는 missing 발생 확률이 missing이 발생하는 변수에 의존하지 않으면, 즉 MCAR과 MAR 가정 하에서는 bias가 발생하지 않습니다. 이 부분은 MAR 파트에서 더 자세히 설명하겠습니다.
  

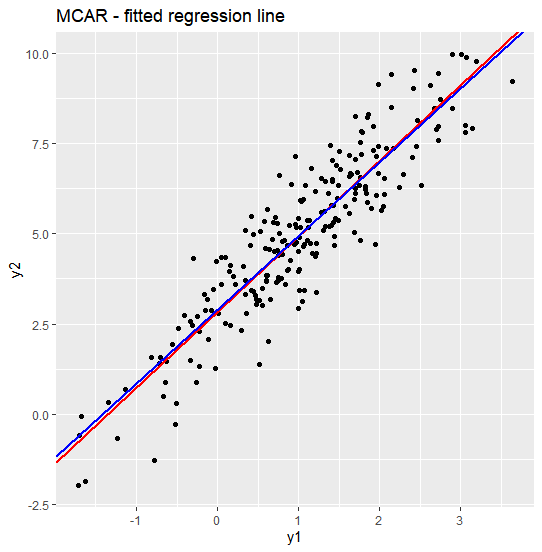
2. MAR(Missing at Random)

MAR 가정은 missing 발생 확률이 관측값에만 의존하고, missing이 발생하지 않는 변수에는 의존하지 않는다는 가정입니다. MCAR의 가정의 가장 큰 단점은 실제 데이터에서 현실적이지 않은 가정 이라는 것입니다. 반면, MAR은 MCAR보다 가정이 완화되었기 때문에, 실제 데이터에서도 자주 쓰이는 가정입니다. 그러면 저희의 sample data에서 MAR가정으로 missing 을 발생시켰을 때, missing data의 분포가 어떻게 되는지 확인해보겠습니다.

# MAR 결측 발생 code
df.full2 = data.frame(cbind(y1,y2))
u2 = 2*(y1-1)+z3
na.idx2 = which(u2<0)
df2 = data.frame(cbind(y1,y2))
df2.complete = df2[-na.idx2,]
df2.incomplete = df2[na.idx2,]
df2[na.idx2,]$y2 = NA

MAR 가정의 정의에 따라, missing 발생 확률은 observed data인 Y1에 의존합니다. 따라서 빨간색 점으로 표시된 결측값들을 보면 MCAR 가정과 달리 전체적으로 퍼져있지 않고 상대적으로 작은 값(2 미만)에서 결측이 발생한 것을 볼 수 있습니다. 이유는 다음과 같습니다. y1은 u에 비례하기 때문에 u가 작아지면 y1도 작아집니다. 그리고 앞서 결측을 u<0 을 만족하면 발생시켰는데, u<0 에 해당하는 y1값들은 상대적으로 작기 때문에 작은 값에서 결측이 발생한 것입니다!

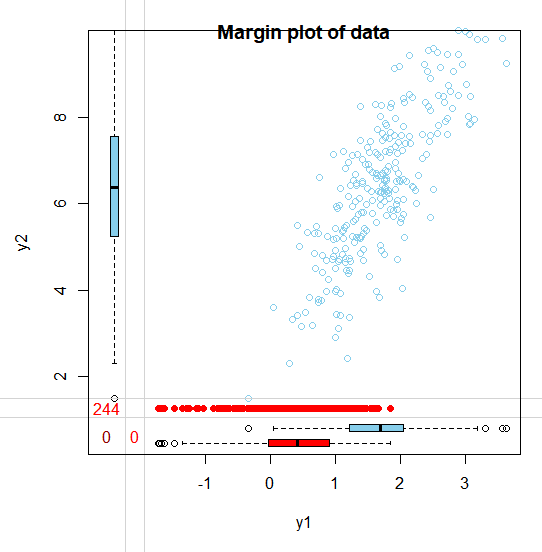
(1) Complete vs Incomplete set

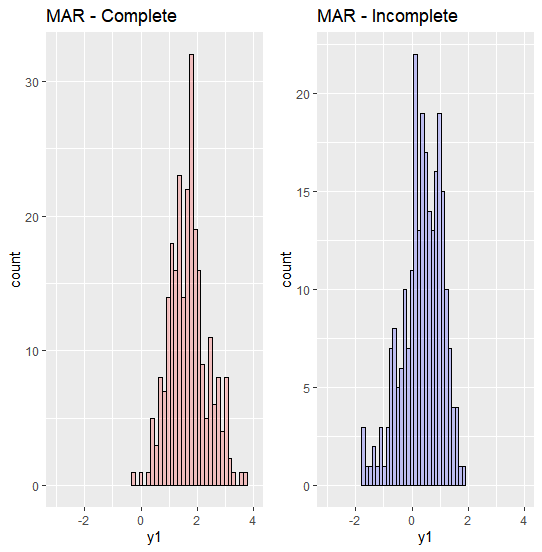
이제 MAR 하의 complete 과 incomplete set의 분포를 비교해보겠습니다. MAR 하에서 y1의 complete, incomplete 의 분포가 확연히 다른 것을 알 수 있습니다. Complete 의 경우 y1의 range가 -1에서 4인 반면, incomplete에서는 y1의 range는 -2에서 2 입니다. 그리고 여기서 알 수 있는 것은, missing이 주로 y1의 작은 값에 해당한다는 것입니다.

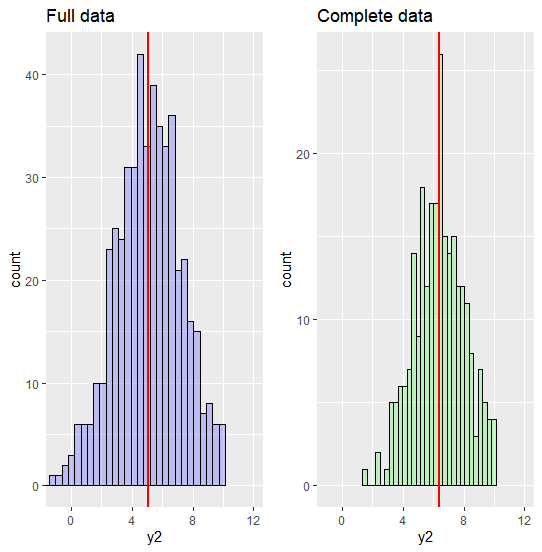
(2) Original vs Complete set - comparing distribution, mean, variance, regression coefficients

원본 데이터와 complete 데이터셋의 y2(missing 발생 변수)를 비교하면 다음과 같은 해석을 할 수 있습니다.
Interpretation

• MAR 가정 하에서는 original data와 complete data의 분포가 다르다. 특히, complete data는 2 이하인 값을 갖고 있지 않다.
• MAR 가정 하에서 original data와 complete data의 분포가 다르므로, mean도 다르다. 즉, mean bias가 발생한다는 것을 알 수 있다.
• Missing은 상대적으로 작은 y2(y1) 값에서 발생한다.

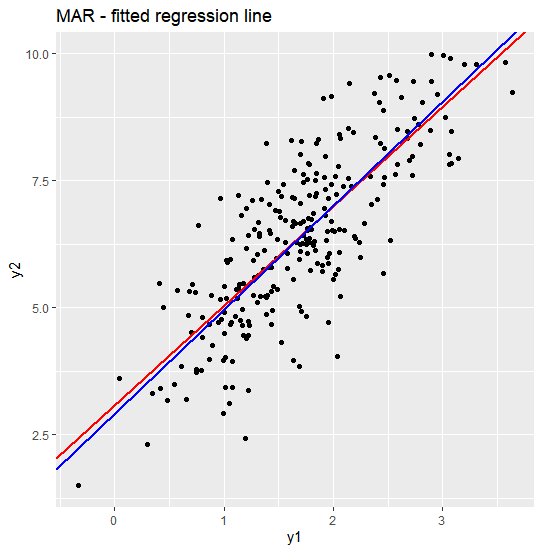
회귀계수 비교

MAR 데이터에서 회귀계수를 비교해보겠습니다. 앞서 MCAR 회귀계수 비교에서도 설명했지만, 이론적으로 complete case에서의 회귀계수 추정값은 missing 발생 확률이 y2에 의존하지 않는다면 bias가 발생하지 않습니다. 즉, MAR 가정은 missing 발생 확률이 y1에만 의존한다고 가정하기 때문에 회귀계수의 complete case estimates는 원본과 다르지 않을 것입니다. 그래프로 봐도 bias가 거의 없다는 것을 알 수 있는 것이죠

3. MNAR(Missing Not at Random)

이제 마지막 missing data mechanism인 MNAR 에 대해 살펴보겠습니다. MNAR은 앞의 두 가정과 달리, missing 발생 확률이 관찰된 값에도, 결측이 발생한 값에도 의존한다고 가정합니다. 이러한 이유로 MNAR 가정 하에서 missing이 발생한 데이터는 분석이 어려운 경향이 있습니다. MNAR 데이터는 다음과 같이 생성합니다.

# MNAR 결측 발생 code
df.full3 = data.frame(cbind(y1,y2))
u3 = 2*(y2-5)+z3
na.idx3 = which(u3<0)
df3 = data.frame(cbind(y1,y2))
df3.complete = df3[-na.idx3,]
df3.incomplete = df3[na.idx3,]
df3[na.idx3,]$y2 = NA

이렇게 MNAR로 생성한 데이터의 missing 분포를 보겠습니다. MNAR에서 missing 발생확률은 y1, y2에 의존합니다. MAR과 마찬가지로 잠재변수 u가 작아지면 y1, y2도 작아지는 경향이 있기 때문에, u<0에서 missing을 발생시키면 y1, y2의 작은 값에서 missing이 발생합니다. (빨간색 점으로 표시)

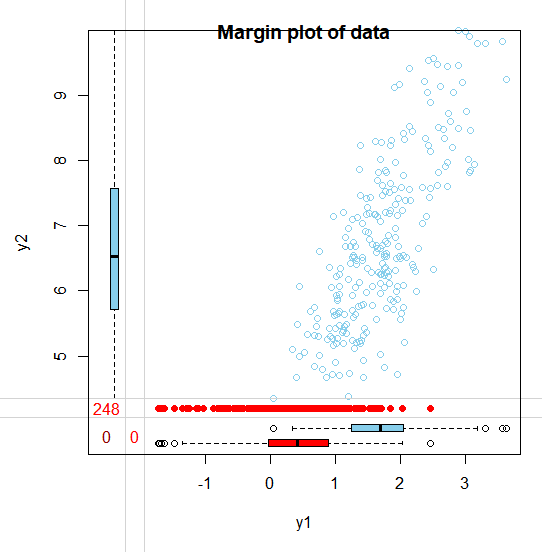
(1) Complete vs Incomplete set

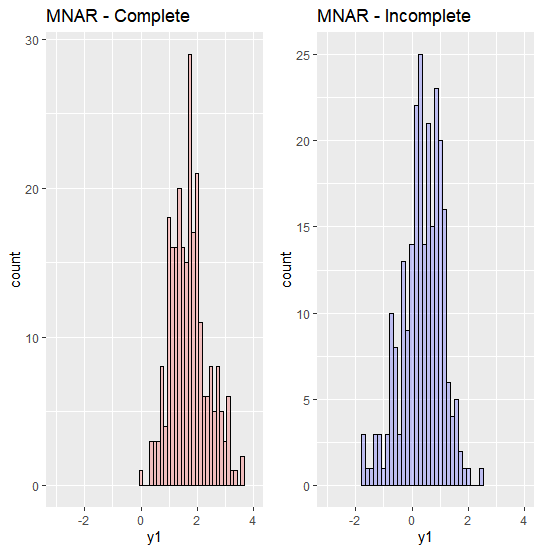
이제 MNAR 하의 complete 과 incomplete set의 분포를 비교해보겠습니다. MAR 하에서 y1의 complete, incomplete 의 분포가 확연히 다른 것을 알 수 있습니다. 이는 MAR과 비슷한 양상을 띄고 있습니다.

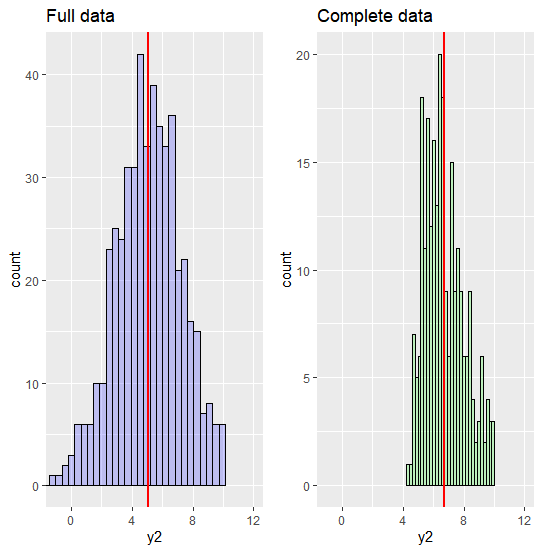
(2) Original vs Complete set - comparing distribution, mean, variance, regression coefficients

원본 데이터와 complete 데이터셋의 y2(missing 발생 변수)를 비교하면 다음과 같은 해석을 할 수 있습니다.
Interpretation

• MNAR 가정 하에서는 original data와 complete data의 분포가 다르다. MNAR에서는 특히 complete set이 MAR보다 범위가 더 제한되어있다. 이는 MNAR이 y2까지 missing 발생 확률에 포함하기 때문에, complete set의 크기가 상대적으로 작아지기 때문이다.
• MAR 가정 하에서 original data와 complete data의 분포와 범위가 다르므로, mean도 다르다. 즉, mean bias가 발생한다는 것을 알 수 있다.
• Missing은 상대적으로 작은 y2(y1) 값에서 발생한다.

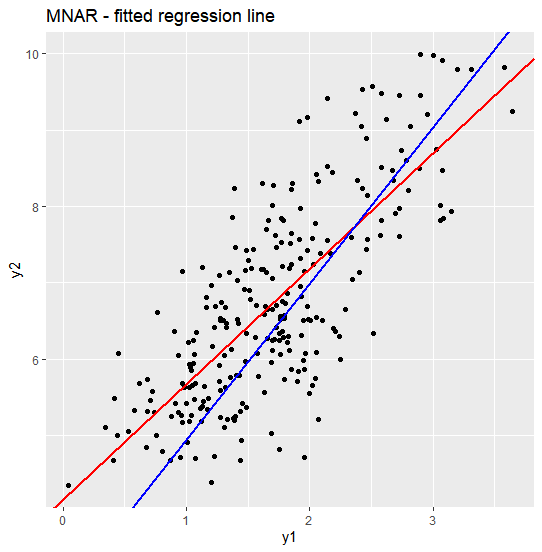
회귀계수 비교

MNAR 데이터에서 회귀계수를 비교해보겠습니다. MNAR에서 missing 발생 확률은 y2에 의존하므로, complete case에서의 회귀계수 추정값은 원래 값과 bias가 발생하게 됩니다. 이는 MNAR과 MAR/MCAR이 구분되는 특징 중 하나이기도 합니다. 그래프에서도 볼 수 있듯이, MNAR 하에서 회귀계수 추정값은 original data 와 complete data에서 차이가 많이 발생합니다.

마무리 < 이렇게 missing data mechanism의 종류와 그 특징에 대해서 그래프와 함께 살펴보았습니다. 긴 글 읽어주셔서 감사합니다 :)