[Time Series Analysis] #1 시계열 평활기법(1)
시계열분석(Time Series Analysis) 은 하나의 변수에 대한 시간에 따른 관측치인 시계열데이터를 분석하는 것이다.
시계열 데이터를 다루는 공모전이 많았는데 나는 비전공자(수학과)에다가 데이터의 길로 입문한지 얼마 되지 않았기 때문에 시계열분석에 대한 지식이 없어서 참가하지 못했던 아쉬움이 있었다.
그래서 이제부터 KMOOC 시계열분석 강의를 듣고 이론을 공부하고, 자율적으로 python에서는 어떤 코드를 써야 하는지 공부하고 포스팅하기로 마음먹었다.
첫번째 주제로는 시계열분석의 기초인 평활기법 에 대해서 리뷰하도록 하겠다. 그리고 각 방법에 해당하는 코드 실습을 첨부한다. 사용한 데이터는 temperature 데이터이다.
Preview
우선 본격적인 이론 및 코드 적용에 앞서, 사용한 데이터에 대해 간단히 살펴보자.
[Data information]
- 1981년 1월 1일부터 1990년 12월 31일까지의 온도 데이터
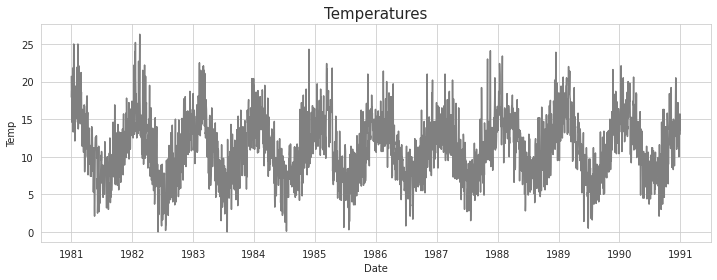
이 데이터셋에는 따로 train, test set이 없지만, 필자는 1990년(총 1년) 데이터를 test set으로 설정해 train set(1981~1989)에 시계열 평활기법을 적용해 test set을 예측하는 방식으로 본 포스팅을 풀어나갈 것이다.
1. 이동평균(Moving Average)
이동평균법 은 매 시점에서 직전 N개의 데이터를 이용해 평균을 구하는 방법이다. 보통 N이 커질수록 평활 정도가 커진다.
수식으로 표현하면 다음과 같다. $M_{t}$를 시점 t에서의 이동평균, $X_{t}$ 를 시점 t에서의 temperature 이라고 하면 $M_{t} = \frac{1}{N}(X_{t}+ \cdots + X_{t-N+1})$ 이다.
이동평균은 생각보다 굉장히 심플한 개념이다. 이제 이를 temperatures 데이터에 적용해보고 N의 크기에 따라 어떤 차이를 보이는지 살펴보자.
Python에서 제공하는 rolling 함수를 이용하면 이동평균을 계산할 수 있다. 여기서 window가 바로 이동평균을 몇 개의 시점에 대해 낼 것인지를 결정하는 N 값이다. Temperature 데이터에
한 달(30일), 1분기(120일), 1년을 기준으로 이동평균을 계산하여 비교하자! 코드는 아래와 같다.
# monthly
temp['window_month'] = temp['Temp'].rolling(window = 30, min_periods=1).mean()
# quaterly
temp['window_quarter'] = temp['Temp'].rolling(window = 120, min_periods=1).mean()
# yearly
temp['window_year'] = temp['Temp'].rolling(window = 365, min_periods=1).mean()
이렇게 추출한 결과를 실제 데이터와 비교하면 다음과 같다. Monthly와 Quarterly로 이동평균을 낸 결과는 실제 데이터의 추세와 계절성을 잘 반영하는 것을 볼 수 있다. 반면 Yearly의 경우 N이 너무 크기 때문에 평활효과가 커져 세부적인 추세는 잘 반영하지 못하는 모습을 보인다.
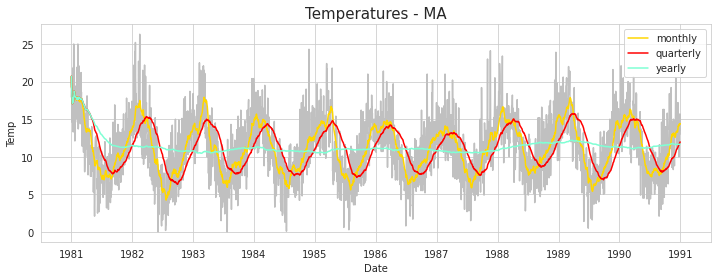
이제 이 세가지 이동평균 중, 추세를 제일 잘 반영하는 Monthly 이동평균을 이용해 test set을 예측해보자. 앞선 코드와 다른 점은, 위 그래프에서는 1990년의 데이터를 이용하여 이동평균을 구했지만, 이제는 train set만의 데이터를 이용해 1990년 데이터의 이동평균을 구한다. 구현한 코드는 아래에 있다.
preds_ma = []
num_train_idx = len(train)
num_test_idx = len(test)
for i in range(len(test)):
idx = num_train_idx + i
rolling = temp.iloc[idx-30:idx,:]
ma = np.round(rolling['Temp'].mean(),1)
preds_ma.append(ma)
결과는 다음과 같다. 이동평균으로 test set을 예측하면 대략적인 추세는 잘 예측하지만, 이동평균의 특성상 세부적인 변동은 반영하지 못하는 것을 알 수 있다.
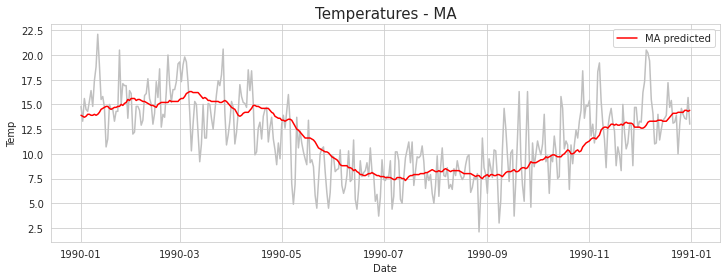
2. 지수평활법(Exponential Smoothing)
지수평활법 은 평활치를 구하는데 시점마다 다른 가중치를 두는 방법이다. 이 때, 현재에 가까울수록 더 큰 가중치를 줌으로써 최근의 추세를 반영하도록 한다. 이 중 단순지수평활법은 수평적인
추세를 반영할 때 사용된다. 선형적인 추세를 반영하는 기법은 뒤 포스트에서 설명하도록 하겠다.
시점 t에서의 지수평활치 수식은 다음과 같다. $S_{t} = \alpha X_{t} + \alpha(1-\alpha) X_{t-1} + \alpha(1-\alpha)^2 X_{t-2} + \cdots$ 로 지수평활치를 구한다. 과거 시점으로 갈수록
$(1-\alpha)$ 의 지수를 하나씩 커지게 함으로써 점점 작은 가중치를 부여한다. ($0<\alpha<1$)
- $\alpha$ 가 커질수록 현재 시점의 값을 더 많이 반영한다.
- $\alpha$ 가 작을수록 평활효과가 크다. $\alpha$ 가 작을수록 전체적인 평균을 반영하려는 경향이 커지기 때문이다.
이제 $\alpha$ 값에 따라 지수평활치가 추세를 어떻게 반영하는지 비교해보자. Python의 SimpleExpSmoothing 함수를 이용하면 단순지수평활법을 적용할 수 있다.
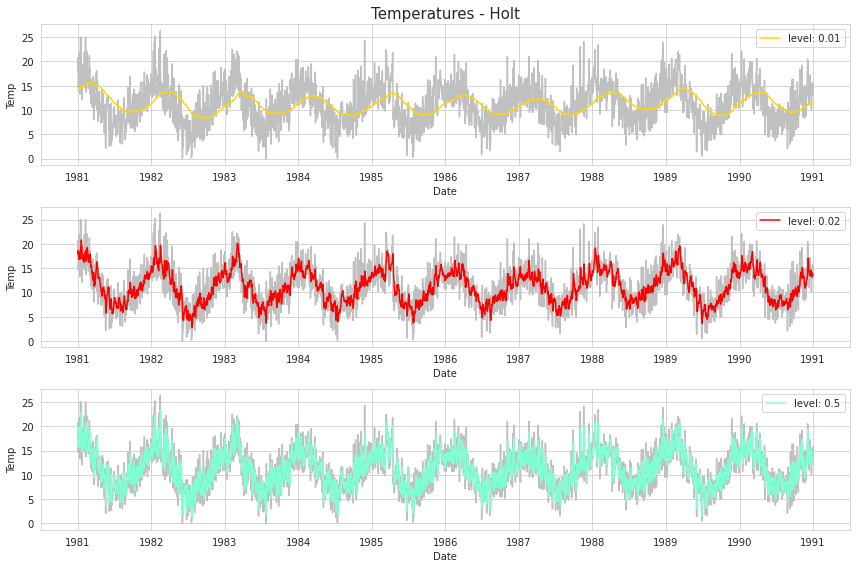
위 그림을 보면 $\alpha$ 가 클수록 각 시점에서의 값을 잘 반영하는 것을 볼 수 있다. 큰 $\alpha$는 현재 시점의 값을 가장 많이 반영하기 때문에 나타나는 결과이다.
세 경우 중 $\alpha$ 가 0.5 일 때 추세를 가장 잘 반영하기 때문에 이를 이용하여 test set의 시계열 값을 예측해보겠다.
# Simple Exponential Smoothing
model = SimpleExpSmoothing(train['Temp']).fit(smoothing_level=0.5) # 단순지수평활 모델 생성
test['SES'] = model2.forecast(365) # 365일의 데이터 forecast
# 결과 plot
plt.figure(figsize=(12,4))
sns.set_style('whitegrid')
sns.lineplot(data=test, x='Date', y='Temp', color='silver')
sns.lineplot(data=test, x='Date', y='SES', color='red', label= 'SES predicted')
plt.title('Temperatures - SES', fontsize=15)
plt.show()
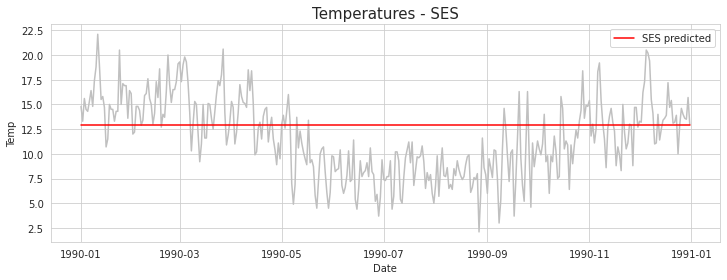단순지수평활법을 적용하여 test set을 예측하면 단순 직선으로, 즉 한가지 값으로만 예측한다. 이는 단순지수평활법은 수평 추세를 반영하는 데 사용되는 기법이기 때문에, temperatures 데이터가
갖고 있는 계절성을 반영하지 못하는 모습을 보인다. 더 중요한 것은, Preview 파트의 원본 temperatures 데이터의 시계열 분포를 보면 Temp가 8-9월 경까지 감소했다가 다시 증가하는 패턴을 보이는데, 전체적으로 봤을 때 추세가 증가한다 혹은 감소한다 라고 정의하지 못한다. (감소한만큼 다시 증가하여 상쇄되기 때문)
여기서 지수평활기법 설명 파트 1을 마무리 짓겠다! 다음에는 홀트, 홀트-윈터스 모형 및 분해법에 대해 알아보도록 하자.
댓글남기기