[Time Series Analysis] #1 시계열 평활기법(2)

이번 포스팅에서는 저번 포스팅에 이어 평활기법 중 Holt 및 Holt-winters 에 대해 다루도록 하겠다. 지난 포스트처럼 이론에 대해 설명한 후, Python code로 실습을 하는 흐름으로 진행하겠다.

1. Holt 와 Holt-Winters, 그리고 그 차이

Holt와 Holt-winters 기법은 비슷한 듯 보이지만 분명한 차이가 존재한다. 그 차이와 각 기법의 이론에 대해 알아보자!

(1) Holt

Holt 모형은 시계열데이터게 추세 패턴을 갖고 있는 경우 적용하는 시계열 지수평활기법이다. 저번 포스팅에서 다룬 단순지수평활법 이 수평 추세 패턴을 갖고 있는 데이터에 적합한 것에 반해, 이 데이터는 선형 등의 추세 패턴을 가진 데이터에 적합한 방법이다. 다만, Holt 모형은 계절성을 반영하지 않는다.
t 시점에서의 Holt 모형은 수평수준(levels)를 나타내는 $L_{t}$ 와 추세(trend)를 나타내는 $b_{t}$ 로 표현할 수 있다. 가령, 시점 t에서 t+k 시점의 값을 예측한 값은 $f_{t}= L_{t} + kb_{t}$ 로 계산한다.

(2) Holt-Winters

Holt-Winters 모형은 Holt 모형이 계절성을 반영하지 못한다는 단점을 보완한 모형이다. 즉, Holt-Winters 모형은 시계열데이터의 추세패턴과 계절성을 모두 반영한다. 이전 평활기법들과 달리, Holt-Winters 모델은 시계열 데이터의 계절성이 어떤 패턴을 보이는지에 따라 Additive(가법) 과 Multiplicative(승법) 으로 나눠진다.

여기서 잠깐! Additive 와 Multiplicative 의 차이는 무엇이고, 계절성의 패턴이 어떤 것에 해당하는지 어떻게 판단할까?

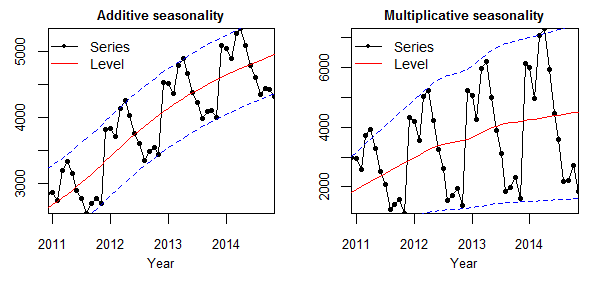
위의 두 가지 그림은 모두 계절성을 띄고 점점 증가하는 추세를 보이고 있다. 차이는 시계열데이터의 진폭 에서 찾을 수 있다. 여기서 말하는 진폭이란, 한 주기에서 고점과 저점의 차이를 말한다. Additive 의 경우 증가 추세를 보이지만, 각 주기마다 진폭이 대체로 일정한 반면, Multiplicative의 경우 각 주기의 진폭이 점차적으로 증가한다.

그러면 다시 본론으로 돌아와 Holt-Winters의 이론에 대해 살펴보자. Holt 모형과 마찬가지로 Holt-Winters 모형은 수평수준(levels) $L_{t}$와 추세(trend) $b_{t}$ 요소를 갖고 있다. 추가적으로 Holt-Winters는 계절성을 반영하기 때문에 이를 나타내는 계절성지수 $s_{t}$ 를 포함한다. (이 때 계절성지수들의 평균은 1이 되도록 조정한다.) 따라서 시점 t에서 시점 t+k의 값을 예측한 값은 다음과 같이 나타낼 수 있다. 두 기법의 차이는 계절성지수 $s_{t-m+k}$ 를 $L_{t}+kb_{t}$ 에 곱했는지 더했는지에 있다.

• Additive: $f_{t,k}=L_{t}+kb_{t}+s_{t-m+k}$
• Multiplicative: $f_{t,k}=(L_{t}+kb_{t})s_{t-m+k}$

2. Python code 실습

이제 실제 데이터를 가지고 본 포스팅에서 다룬 기법들을 적용해보자! 저번 포스팅에서 사용한 데이터는 계절성은 보이지만, 추세 패턴은 보이지 않아서 아쉬웠다. 따라서 이번엔 다른 데이터를 사용해서 실습을 해보겠다.

(1) Data Information

• 기간: 1992년 1월 1일 ~ 2020년 1월 4일
• 일별 Retail Sales 데이터
• 추세(trend): 대체로 증가하는 추세 보임
• 계절성: 1) 1년 단위로 봤을 때, 연말로 갈수록 증가하는 계절성을 보임 2) 각 주기마다 진폭이 점점 증가하기 때문에 Multiplicative 모형 적용 필요

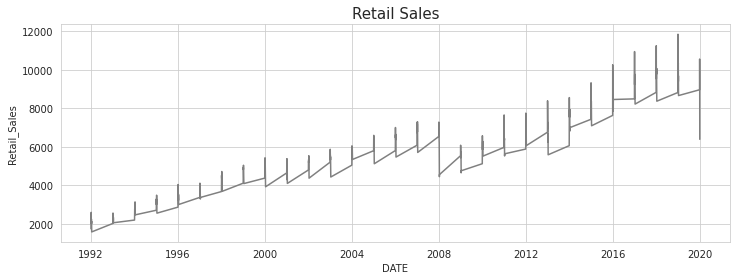
이렇게 데이터의 기본적인 정보와 패턴을 파악했다. 본 포스팅에서는 두 모형의 예측 성능 비교를 위해 2016년 1월 1일 이후의 데이터를 test set으로, 이전의 데이터를 train set으로 지정하여 train set으로 학습시킨 뒤 test set을 예측하는 방식으로 진행겠다!

(2) Holt

우선 Holt 모형을 Retail Sales 데이터에 적용해보자. Python의 Holt 함수를 이용하면 구현할 수 있다. 이 때 input 중 smoothing_level 인 $\alpha$를 설정하는데, 이에 대한 설명은 저번 포스팅 에서 다루었다. $\alpha$ 값에 따라 fitting이 얼마나 잘 되는지 비교해보자.

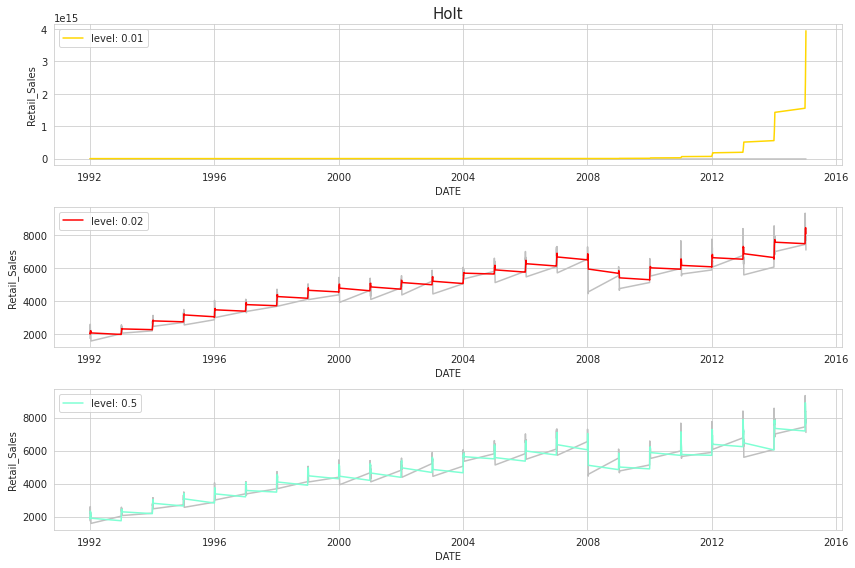
역시 $\alpha$가 클수록 현재 시점의 데이터의 가중치를 더 크게 부여하기 때문에, fitting 성능이 더 좋다는 것을 확인할 수 있다.

이제 train set을 이용해 test set의 Retail Sales 를 예측한다. Holt 함수에 내장되어 있는 forecast 를 사용하면 된다. 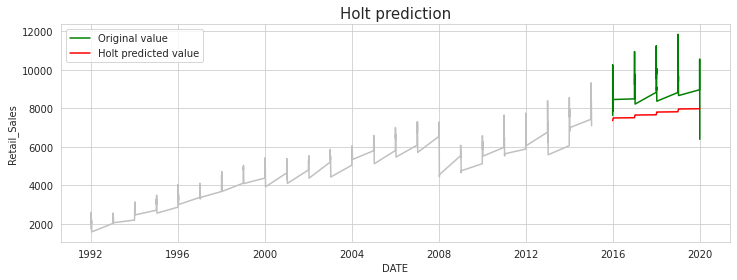[해석]
Predicted value는 원본 데이터의 증가 추세는 반영했지만, 1년 단위로 연말로 갈수록 점점 Retail Sales가 증가하는 계절성은 반영하지 못한다. 예측값들은 대체적으로 선형 추세 를 보이고 있는데, 이는 Holt 모형의 예측식인 $f_{t}= L_{t} + kb_{t}$ 가 반영된 결과라고 볼 수 있다.

(3) Holt-Winters

Holt-Winters 모형은 Python의 ExponentialSmoothing 을 사용하여 구현한다. 이 함수를 사용할 때는 몇가지 설정해야할 파라미터가 있다.

• seasonal_periods: 주기 사이클 내의 기간의 수를 숫자로 지정한다. ex) 일주일 주기의 daily 데이터: 7, 일년 주기의 monthly 데이터: 12
• seasonal: additive/multiplicative. 본 분석의 경우 multiplicative 적용
• trend: add/mul. 추세를 나타내는 $b_{t}$는 더해지기 때문에 add 적용

파라미터를 지정했으면 본격적으로 분석을 한다. 이 때 seasonal_periods는 본 데이터가 일년 주기의 계절성을 띄므로 4(분기별), 12(월별) 를 각각 적용해 그 결과를 비교했다.

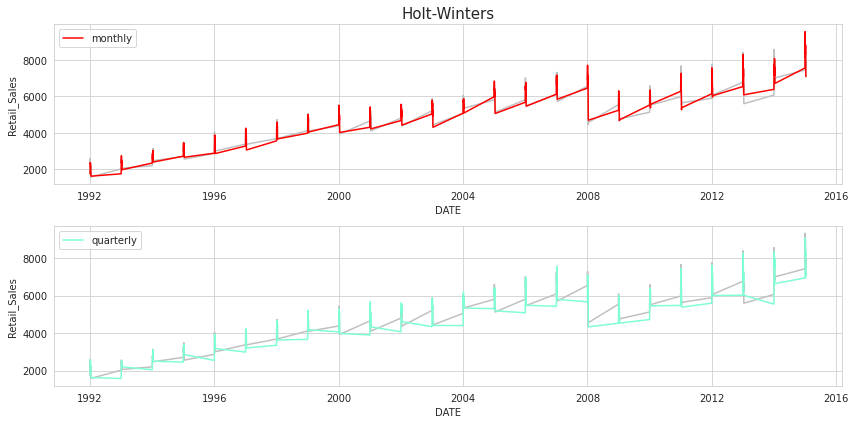
월별로 예측한 데이터가 원래 시계열 데이터의 패턴을 잘 fitting 하는 경향을 보인다. 월별로 나눠서 예측을 했을 때가 각 시점의 시계열 데이터를 더 세밀하게 반영하기 때문이다.

그러면 seasonal_periods를 12로 지정하여 test set을 예측해보자. 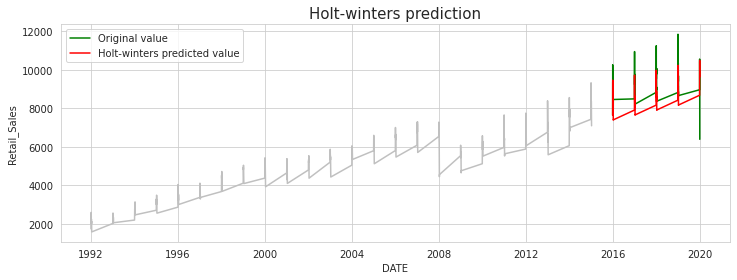[해석]
Holt-Winters는 Holt 모형보다 훨씬 원본 데이터에 가깝게 예측하는 것을 확인할 수 있다. Holt 모형이 증가 추세는 예측하지만 계절성은 전혀 예측하지 못하는 것에 비해 Holt-Winters 모형은 증가 추세와 연말로 갈수록 증가하는 계절성을 모두 capture 했다! 또한 seasonal을 multiplicative로 지정했기 때문에, 점점 커지는 진폭의 추세도 대체적으로 잘 반영한 것으로 보인다.

이렇게 Holt와 Holt-winters 모형에 대해 정리하고 Python을 이용해 실습을 해보았다. 여기서 시계열 평활기법에 대한 포스팅은 마무리하고, ARMA 모형 및 이를 이해하는데 필요한 개념에 대한 포스팅으로 돌아오겠다! 포스팅에 사용한 코드는 이곳 에 있다.

---

참고문헌
KMOOC 시계열분석 강의
Additive vs Multiplicative 그래프: https://kourentzes.com/forecasting/2014/11/09/additive-and-multiplicative-seasonality/
https://machinelearningmastery.com/exponential-smoothing-for-time-series-forecasting-in-python/