[Time Series Analysis] #2 ARMA/ARIMA를 위한 개념 Build-up

이제 시계열분석의 핵심 모델인 ARMA/ARIMA를 위한 개념을 잡는 마지막 관문이다! 앞선 두 포스팅에서는 시계열 평활기법에 대해 살펴보았다. 이번 포스팅에서 다룰 내용은 다음과 같다.

1. 정상성 시계열
2. 자기상관함수(ACF)/편자기상관함수(PACF)
3. AR 모델/MA 모델

1. 정상성 시계열(Stationary Time Series)

정상성 시계열 간단하게 말하면 시계열 데이터 ${Z_{t}}$의 expectation과 variance가 일정한 경우를 말한다. 이 때, 정상성 시계열은 조건에 따라 강 정상성(Strong Stationary)와 약정상성(Weak Stationary) 로 분류할 수 있다.

• 강 정상성 1) $(Z_{1},\cdots,Z_{t})$ 와 $(Z_{1+k},\cdots,Z_{t+k})$ 가 같은 결합확률분포를 가진다. 2) $E(Z_{t})$ 는 항상 일정 3) $Var(Z_{t})$ 는 항상 일정 4) $Cov(Z_{t},Z_{t+1}) = Cov(Z_{t+k},Z_{t+k+1})$ : 두 시점의 공분산은 time lag에만 의존한다.

하지만 강정상성의 조건을 만족하는 실제 데이터는 거의 존재하지 않는다. 따라서 좀 더 약한 조건을 적용하는데, 이것이 약 정상성이다.

• 약정상성 1) $E(Z_{t})$ 는 항상 일정 2) $Cov(Z_{t},Z_{s})$ 는 두 시점의 차이의 절대값인 $|s-t|$ 에만 의존한다.

2. ACF/PACF

(1) 자기상관함수(ACF)

ACF는 쉽게 말하면 시계열 데이터 ${Z_{t}}$ 에서 시점 t와 시점 t+k 가 얼마나 상관성이 있는지를 나타내는 함수이다. 시계열데이터분석을 할 때, 이전 시점의 데이터가 현재 시점의 데이터에 미치는 영향을 파악하는 것이 중요하다. 이를 영향을 설명할 수 있는 함수 중 하나가 ACF 라는 것이다!
ACF 수식 표현: $\rho(k) = Cor(Z_{t},Z_{t+k})$

(2) 편자기상관함수(PACF)

PACF는 시계열 데이터 ${Z_{t}}$ 에서 시점 t와 시점 t+k의 관계를 두 시점 사이에 있는 시점 데이터($Z_{t+1},\cdots,Z_{t+k-1}$)를 고려하여 설명하는 함수이다.
ACF 수식 표현: $\rho(k) = Cor[Z_{t},Z_{t+k}|Z_{t+1},\cdots,Z_{t+k-1}]$

3. AR vs MA 모델

두 모델은 모두 정상성을 만족하는 모델이다!

(1) 자기회귀모델(Autoregression Model)

자기회귀모델을 줄여서 AR 모델이라고 통상적으로 칭한다. 시계열 데이터에서 시점 t의 값 $Z_{t}$를 예측할 때, 이전 시점의 값들과 백색잡음(white noise)을 이용하여 예측하는 모델이다. 간단하게 수식으로 나타내면 $Z_{t} = \phi_{1}Z_{t-1}+\cdots+a_{t}$ 이다. 즉, $Z_{t}$ 를 반응변수로, 나머지 이전 시점의 값들을 설명변수로 설정하는 일종의 회귀모델이기 때문에 자기회귀모델이라고 칭하는 것이다!

AR 모델은 일반화하면 AR(p) 로 나타내는데, 여기서 p는 $Z_{t}$를 예측할 때 t 시점을 기준으로 p개의 이전 시점의 값들을 이용한다는 뜻이다. 즉, $Z_{t} = \phi_{1}Z_{t-1}+\cdots+\phi_{p}Z_{t-p}+a_{t}$ 를 만족한다. 이 때, 정상성을 만족하기 위해 계수들은 모두 $-1<\phi_{p}<1,\phi_{1}+\cdots+\phi_{p}<1,\phi_{1}-\cdots-\phi_{p}<1 $ 조건을 만족해야 한다.

AR 모델의 ACF/PACF

AR 모델의 ACF와 PACF plot은 확연히 다른 양상을 띈다. 예시로 KMOOC 강의자료에 있는 그래프를 가져왔다!
AR(1) $Z_{t}=\phi_{1}Z_{t-1}+a_{t}$
[그래프 해석]

• ACF: 지수적으로 감소하는 경향
• PACF: lag 1 이후로 절단된 패턴을 보인다(절단: lag 1 이후로 PACF 값 = 0)
  

즉 일반화하면 AR(p)의 ACF는 지수적으로 감소하는 패턴을 보이지만, PACF는 lag p 이후로 절단된 패턴을 보인다.
하지만 현실세계에서 PACF가 완전히 절단되는 AR 모델은 존재하기 힘들다. 그러면 어떤 기준으로 절단을 정의할 수 있을지 예시를 같이 보자! R 을 이용하면 arima.sim 이라는 함수를 통해 AR 모델에 적합한 예시 데이터를 생성할 수 있다. 필자는 여기서 $p = 1, 2, 3, 4$ 인 경우를 비교해보았다.

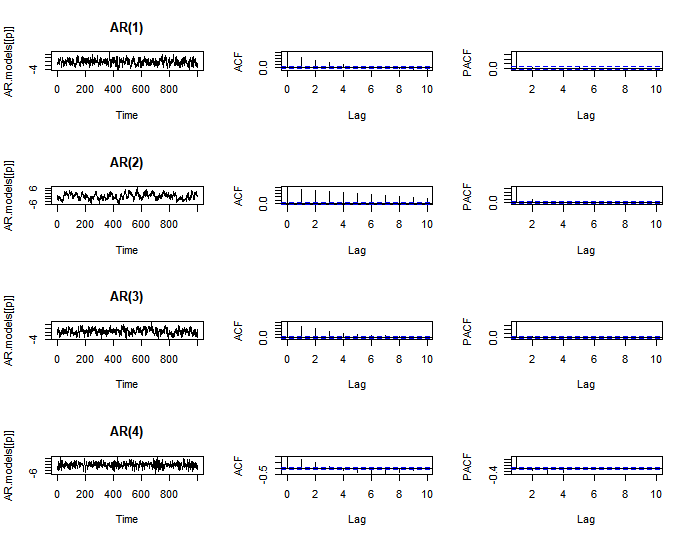[그래프 해석]

• ACF: $p = 1, 2, 3, 4$ 모두 지수적으로 감소
• PACF: 각 p에서 처음 p개의 값은 개별적인 값을 가지지만, p+1 번째 값 부터 급격히 작아진 값을 갖기 시작한다.
  

일반적으로 ACF와 PACF 그래프를 해석할 때, 유의수준 5% 를 나타내는 파란색 선보다 작은 값을 가지면 절단된 것으로 판단한다!

(2) 이동평균모델(Moving Average Model)

이동평균모델은 줄여서 MA 모델이라고 한다. MA 모델의 경우 $Z_{t}$ 를 시점 t에서의 백색잡음과 이전 시점들의 백색잡음을 이용하여 예측한다. 수식으로 표현하면 $Z_{t} = a_{t}-\theta_{1}a_{t-1}-\cdots-\theta_{q}a_{t-q}$ 이다. 정상성을 만족하기 위해 계수들은 모두 $-1<\theta_{q}<1,\theta_{1}+\cdots+\theta_{q}<1,\theta_{1}-\cdots-\theta_{q}<1 $ 조건을 만족해야 한다.

MA 모델의 ACF/PACF

MA 모델의 ACF와 PACF plot을 살펴보자. MA(1) $Z_{t}=a_{t}-\theta_{1}a_{t-1}$
[그래프 해석]

• ACF: lag 1 이후로 절단된 패턴을 보인다(절단: lag 1 이후로 ACF 값 = 0)
• PACF: 지수적으로 감소하는 경향
  

즉 일반화하면 MA(q)의 PACF는 지수적으로 감소하는 패턴을 보이지만, ACF는 lag p 이후로 절단된 패턴을 보인다.

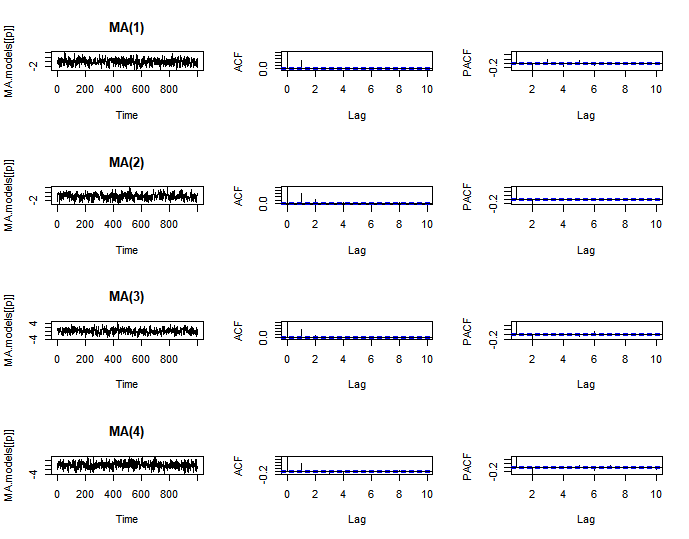[그래프 해석]

• ACF: 각 p에서 처음 p개의 값은 개별적인 값을 가지지만, p+1 번째 값 부터 급격히 작아진 값을 갖기 시작한다.
• PACF: $p = 1, 2, 3, 4$ 모두 지수적으로 감소
  

---