[Time Series Analysis] #4. Simple Web Traffic Data Analysis - Part 2
Kaggle data에 시계열분석 적용해보기
Part 2: ARIMA application
지난 포스트에서는 Web Traffic 데이터에 대한 EDA를 진행했다. 이번 포스트에서는 시계열분석이론에서 공부했던 ARIMA 모델을 적용한 결과를 다룬다!
일단 결론부터 말하자면… ARIMA를 이용한 Web Traffic 데이터 예측의 성능은 매우매우 좋지 않았다..! 그래서 이번 포스트에서는 왜 성능이 안좋았는지에 대해서 나름 생각해본 부분도
다뤄보도록 하겠다.
1. 세부 데이터 선택
저번 포스트에서 Page 별로 클러스터링을 했을 때 클러스터 4에 속하는 Page의 추세가 전체적인 추세와 가장 비슷하다는 결과를 얻을 수 있었다. 따라서 ARIMA 모델 분석을 위해, 클러스터 4에
속하는 데이터 중 평균 Visits 수가 가장 높은 Page를 선정했다. 해당 Page는 ‘메인 페이지’로 위키피디아 홈페이지에 접속하면 가장 먼저 뜨는 페이지이다.(그러니 당연히 평균 방문수가 높을 것이다.)
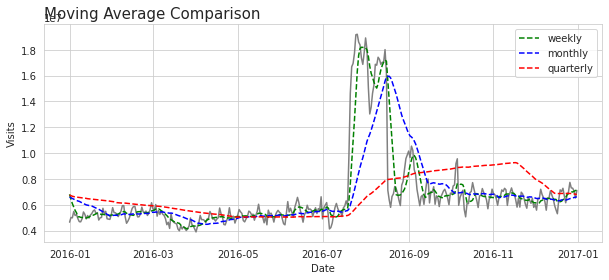
메인 페이지 방문 수는 곧 위키피디아 방문 수를 대변할 수 있기 때문에 이 데이터를 활용해보겠다. 아래 그래프는 메인 페이지의 날짜별 방문 수와 weekly, monthly, quarterly 이동평균을 그려본 plot이다.
2. ARIMA
ARIMA 모델링의 순서는 다음과 같다.
- 분산 안정화(Variance Stabilization)
- 시계열의 정상성(Stationary) 여부 확인
- ADF test(단위근 검정)
- ACF graph
- 차분(Differencing)
- ARIMA 모델링
(1) 분산 안정화(Variance Stabilization)
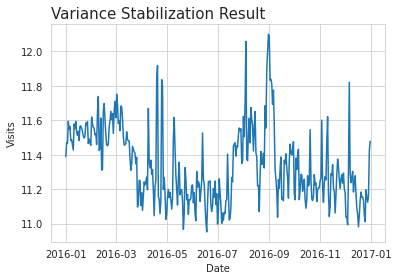
시계열분석을 하기 전, 시계열 데이터가 정상성을 만족하는지를 먼저 확인해야 한다. 시계열 데이터의 시점 별 평균, 분산이 시점에 관계없이 일정할 때 이 데이터는 정상성을 만족한다고 말한다. 하지만 위 메인 페이지 데이터 그래프를 보면, 데이터의 분산이 일정하지 않고 들쭉날쭉한 것을 볼 수 있다. 따라서 본격적인 정상성 테스트 전, 적절한 변환을 이용해서 시계열데이터의 분산을 정상화 처리를 해줘야 한다. 본 데이터에서는 Log transformation 을 적용했다. 아래 그래프를 보면 로그변환 결과 분산이 어느정도 비슷하게 변환된것을 볼 수 있다.
(2) 정상성 여부 검정
1) ADF test
시계열데이터의 정상성을 검정하기 위해서는 여러가지 방법을 활용할 수 있는데, 가장 대표적인 것이 ADF test(단위근 검정)이다. 이 검정의 귀무가설은 $H_{0}: \phi = 1$ 이다. 만약
검정통계량이 커서 p-value가 유의수준 5%보다 작으면 귀무가설을 기각하는데, 귀무가설을 기각하면 시계열데이터가 정상성을 만족한다고 판별한다.
|statistics|value|
|——|—|
|ADF|-1.328|
|p-value|0.6160|
위 표는 메인페이지 데이터의 ADF 검정 결과를 보여준다. p-value가 0.6160으로 유의수준 5%보다 크기 때문에 귀무가설을 기각하지 못한다. 따라서 메인페이지 데이터는 비정상적 시계열 특성을 갖고 있다고 결론을 내릴 수 있다.
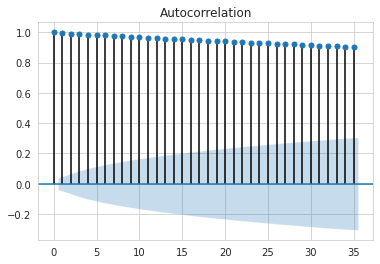
2) ACF
정상성여부를 확인하기 위한 또 다른 방법은 ACF 그래프를 이용하는 것이다. 만약 시계열데이터가 정상성을 만족하면 ACF 값들은 지수적으로 감소하는 반면, 비정상성을 만족한다면 ACF가 감소하는 속도는 매우 느리다.
메인페이지 데이터의 ACF는 매우 느리게 감소하기 때문에 이 역시 메인페이지 데이터가 비정상성을 만족한다는 가설을 뒷받침해준다.
(3) 차분(Differncing)
그러면 비정상성 시계열을 어떻게 정상성을 만족시킬 수 있도록 바꿀까? 가장 대표적인 방법은 차분을 이용하는 것이다. 차분이란, 쉽게 말하면 시점 t와 t-1의 시계열데이터의 차이라고 보면 된다. 차분은 1차, 2차, 3차 이렇게 n번 차분을 할 수 있는데, 이 n은 n번 차분을 한 데이터가 처음으로 정상성을 만족하는가를 판단하여 정하면 된다.
이제 우리 데이터에 차분을 적용해보자. Python에서는 그냥 diff() 를 적용해주면 끝난다. 만약 두번 차분하고 싶으면 diff().diff() 를 시행해주면 된다!
1) 1차 차분 후 PACF
1차 차분 후 시계열데이터의 분포와 PACF를 나타낸 것이다. 시계열데이터는 추세, 계절성을 보이지 않기 때문에 어느정도 정상화가 됐다고 예상할 수 있다. PACF를 보면 PACF 값들은 지수적으로 감소하고 특히 lag 1 이후로 5% 유의한계선 안에 값들이 들어가기 때문에 메인페이지 데이터는 AR(1) 을 만족할 것이라고 예상할 수 있다.
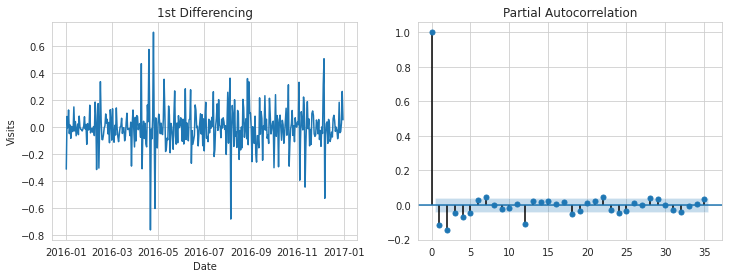
2) 1차 차분 후 ACF
1차 차분 후 ACF 역시 지수적으로 감소하는 경향을 보이며 lag 1 혹은 2 이후로 ACF 값들이 5% 유의한계선 밑으로 떨어지기 때문에 메인페이지 데이터는 MA(1) 모델이 적용될 것이라고
예상할 수 있다.
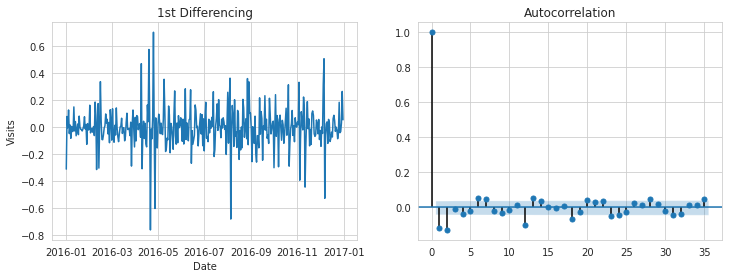
3) ADF test
그래프만으로는 정상성 여부를 판단할 때 확실하지 않기 때문에 ADF test를 다시 한번 시행한다. 그 결과, p-value는 유의수준 5%보다 작기 때문에 정상성을 만족한다고 결론내릴 수 있다! 즉 메인페이지 데이터는 1차 차분만으로도 정상성 시계열 데이터로 변환 가능하다.
(4) ARIMA 모델링
파트 (3)에서 차분을 통해 우리는 ARIMA 모델의 차수 $(p,d,q) = (1,1,1)$ 를 만족한다고 예상할 수 있었다. (여기서 p는 AR 모델이 포함하는 이전 시점의 수, d는 차분 수, q는 MA 모델이 고려하는 이전 white noise 수) 이제 ARIMA 모델을 학습해보고 결과를 보자.
- ARIMA(1,1,1) 모델을 통해 나온 coefficients 로 얻은 모델 식: $Z_{t} = 8.63Z_{t-1} + 13.527a_{t-1}$ (상수항의 p-value는 0.9 이상으로 유의미하지 않으므로 제거한다)
- AIC = 3345 로 매우 크다. AIC는 작을수록 성능이 좋은데, 일단 여기서부터 ARIMA 모델은 메인페이지 데이터에 적합하지 않은 것을 알았다..
Auto_arima
파트 (3)에서 차분을 해 보았는데, AR와 MA 차수를 그래프만을 이용해 결정하는 것이 다소 헷갈리는 부분이 있었다. Python에서는 auto_arima 라는 함수를 제공하는데 이를 이용하면 다양한 조합의 p, q를 ARIMA 모델에 적용해 가장 좋은 성능을 내는 $(p,q)$의 조합을 찾을수 있다.
- Auto_arima 를 통해 얻은 가장 성능이 좋은 ARIMA 모델은 ARIMA(0,1,2) 이다. 이는 앞서 우리가 그래프를 통해 해석한 결과와 다르다.
White noise 검정
ARIMA 모델에서 중요한 조건 중 하나는, 백색 소음(White noise)가 정규분포를 따르며 독립적이고 랜덤하게 발생한다는 가정이다. 우리가 구한 메인페이지 데이터의 ARIMA 모델의 백색소음이
이 가정을 만족하는지 그래프를 통해 확인해보자.
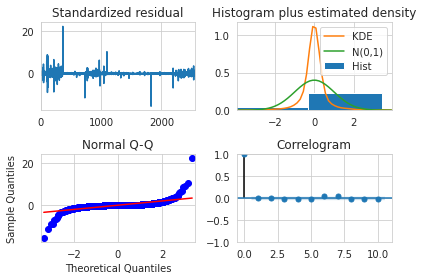
- 1번째 그래프: Residual의 분포가 특정 패턴을 보이지 않고 대체로 랜덤하게 분포한다.
- 2번째 그래프: Residual의 히스토그램이 정규분포를 따르지 않는다.
- 3번째 그래프: Residual에 Normality test를 적용한 결과 normality 직선상에서 벗어나기 때문에 정규성을 만족한다고 볼 수 없다.
- 4번째 그래프: correlogram plot의 값들이 거의 0에 가까우므로, residual 끼리 correlation이 거의 0이고 독립이라는 것을 알 수 있다 그래프를 봤을 때, white noise는 ARIMA 모델에 필요한 가정을 만족하지 못한다.
Web traffic 데이터 중 Main page 데이터에 ARIMA를 적용해봤는데, 예상한 것과 달리 ARIMA의 성능이 좋지 않았다. 그 이유를 몇가지 생각해보았는데
- seasonal decompose plot에선 계절성이 있다고 하나 그래프에서는 뚜렷한 계절성을 찾을 수 없음
- 정상성을 맞추기 위해 변환을 해도 분산의 안정화가 조금 더 될 뿐, 분산이 시간에 따라 일정하지 않음
이렇게 될 것 같다. 이 포스팅을 하기 위해 ARIMA에 대한 수많은 예시들, 문헌들을 찾아보았는데 대부분 사용한 데이터가 뚜렷한 추세와 계절성을 띄는 경우가 많았다. Web traffic 데이터의 경우 데이터가 뚜렷한 추세와 계절성을 띄지 않지만 정상성은 또 만족하지 않는 경우였기 때문에 ARIMA의 결과가 좋지 않았다고 예상된다.
하지만 내 지식이 짧아 방도를 못 찾은 것일수도 있으니 앞으로 더 공부해보면서 원인을 해결해보려고 노력해야겠다!


댓글남기기