[Interpretable ML] #1. Partial Dependence Plot(PDP)

최근에 마친 포스팅 시리즈인 Feature Selection 파트를 준비하면서 자연스럽게 머신러닝의 해석에 관한 이론들도 접하게 되었다. 머신러닝 모델링을 할 때 중요한 feature만을 선택해 모델의 성능을 높이는 것도 중요하지만, 더 나아가 완성된 모델을 어떻게 해석할 것인지가 관건이다. 예를 들어 분류 모델에서 단순히 데이터들을 0, 1, 2로 분류하는 것에서 끝나는 것이 아니라, 어떤 변수가 데이터가 1로 분류되는데에 어떤 영향을 미쳤는지, 변수간의 interaction은 어떻게 되는지 등등을 해석하는 것이 중요하다. (머신러닝 모델에 대한 해석은 비단 모델링 성능을 높이는 데에만 기여하는 것이 아니라 다른 insight를 얻는 데에도 기여할 수 있다.)

머신러닝의 해석 첫 포스팅에서는 머신러닝 해석에 가장 기본적으로 사용되는 plot인 Partial Dependence Plot 에 대해 다루도록 하겠다.

Partial Dependence Plot

PDP는 특정 feature가 target에 미치는 한계효과(marginal effect)를 파악하고자 할 때 사용하는 plot이다. 간단히 수식으로 먼저 살펴보자! Partial dependence function은 다음과 같이 정의된다.(Marginal distribution을 구하는 식과 꽤나 비슷한 걸 확인할 수 있다) $ \hat{f_{x_{S}}} = \frac{1}{n} \sum_{i=1}^{n} \hat{f}(x_{S}, x_{C}^{(i)}) $
여기서 $ x_{C}$는 PDP에서 해석하고자하는 feature set을 나타내고 나머지 해석에 관심이 없는 변수들의 set은 $x_{C}$로 나타낸다. 그리고 $x_{C}^{(i)}$ 는 주어진 데이터가 총 $n$개 일 때, $i$번째 데이터의 관심대상이 아닌 변수들의 set을 나타낸다. 즉 이 함수는 각 데이터셋에서 $x_{S}$의 marginal effect를 계산하고 평균을 냄으로써 $x_{C}$가 target value에 미치는 global한 한계효과를 계산한다.

PDP를 사용할 때 주의해야 할 점은 partial dependence function을 구할 때 $x_{S}$와 $x_{C}$는 독립이어야 한다. 이 독립성에 대한 가정이 PDP의 단점이기도 한데, 그 부분은 뒷부분에서 설명하도록 하겠다.

이제 PDP 기법을 python으로 House Price 데이터에 적용해보고 각 plot을 해석해보자.

(1) 개별 변수의 PDP

PDP로 기본적으로 해석할 수 있는 것은 개별 변수와 target value와의 관계이다. 이 때 PDP가 더 특별한 이유는 인과관계 를 추론할 수 있기 때문이다. Feature importance, Permutation importance와 같은 다른 방법들은 변수들과의 상관관계 정도만 설명이 가능했지만, PDP를 이용하면 특정 변수와 target변수의 인과관계를 해석할 수 있다.

House Price 데이터에서 target은 Sale Price(판매가)이다. 예시로 전체적인 집의 질을 등급으로 나타내는 OverallQual 변수와 집이 지어진 연도를 나타내는 YearBuilt가 Sale Price와 어떤 관계를 가지는지를 PDP로 어떻게 해석할 수 있는지 살펴보자.

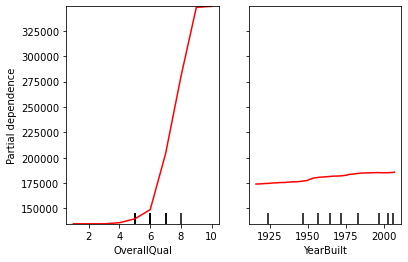
1. OverallQual은 1 ~ 10 으로 집의 등급을 나타내는데, 높을수록 집의 질이 좋은 것이다. OverallQual과 Sale Price에 대한 PDP를 보면 OverallQual이 6이상이 되면 Sale Price아 급격히 상승하는 것을 볼 수 있다. 요약해서 말하면, OverallQUal이 높아질수록(집의 질이 좋을수록) 집의 Sale Price는 증가하는데, 특히 Quality가 6등급 이상이면 Sale Price가 기하급수적으로 높아진다. 즉, OverallQual과 Sale Price는 양의 상관관계를 갖는다.
2. YearBuilt는 집이 지어진 연도를 나타낸다. 1번의 OverallQual 만큼 드라마틱한 변화는 없지만, 오래된 집 보다는 최근에 지어진 집일수록 Sale Price가 높아지는 것을 확인할 수 있다.

이렇게 PDP를 통해 개별 변수가 target 변수와 어떤 관계성을 갖고 있는지를 해석할 수 있다.

Python에서는 다음과 같이 구현할 수 있다.

from sklearn.inspection import plot_partial_dependence # PDP를 위해 필요한 패키지 로드
features = [3, 5] # feature columns index  정(대신 feautre명으로 지정해도 무방하다)
plot_partial_dependence(model, X_train, features, line_kw={"color": "red"})

(2) Interaction effect

PDP로 두 변수 사이의 interaction effect를 확인할 수 있는 plot을 그릴 수 있다. 예시로 OverallQual과 GrLivArea(Above grade living area square feet)의 interaction 양상을 알아보자.

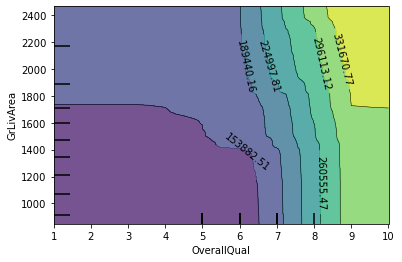
• contour의 색이 밝아질수록 y축에 표시된 변수의 값이 크다는 것을 의미한다.
• 그래프에서 OverallQual이 6 이하일 때는 contour 색이 가장 진한, 즉 GrLivArea가 작다. 하지만 OverallQual이 크면 작은 값에 비해 상대적으로 contour색이 밝아져 GrLivArea가 넓어진다고 해석할 수 있다. 즉, 양의 상관관계를 갖는다.

여기서 주의할 점이 하나 더 있는데, interaction effect는 반드시 인과관계를 의미한다고 단정지을 수 없다. 위 예시에서 OverallQual과 GrLivArea가 양의 상관관계를 갖는다고 해석할 수 있지만, “OverallQual 이 커지먼 GrLivArea가 넓어진다” 라는 casuality를 설명할 순 없다.

from sklearn.inspection import plot_partial_dependence # PDP를 위해 필요한 패키지 로드
features = [('OverallQual', 'GrLivArea')]  # interaction을 살펴보고 싶은 두 변수명을 tuple 형태로 지정
plot_partial_dependence(model, X_train, features, line_kw={"color": "red"})

(3) Model Comparison

PDP를 이용하면 여러가지 모델에서의 개별 변수와 target 변수와의 관계성을 비교할 수 있다. 앞서 우리는 RandomForestRegressor 모델을 사용했는데, 추가적으로 또 다른 트리기반 모델인 LGBMRegressor도 사용하여 PDP를 비교해보자.

1. OverallQual, GrLivArea 둘 다 큰 값으로 갈수록 Sale Price는 랜덤포레스트가 LightGBM보다 가파르게 증가한다.
2. 특정 지점(OverallQual = 6.xx, GrLivArea = 1400) 이전까지는 LightGBM에서 예측한 Sale Price는 랜덤포레스트보다 작지만, 이 지점이 지나면 랜덤포레스트가 LightGBM보다 Sale Price를 높게 예측한다.
3. 전체적으로 그래프를 봤을 때, LightGBM이 랜덤포레스트보다 OverallQual, GrLivArea에 있어서는 더 안정적이라고 볼 수 있다. 랜덤포레스트의 경우, 특정 지점에서 급격하게 값이 변하기 때문에 만약 noise나 outlier가 있을 경우 이들에 LightGBM보다 크게 영향을 받을 것이다.

PDP의 한계

PDP를 통해 개별 변수와 target 변수와의 관계를 해석하고 변수간 interaction도 해석할 수 있지만, 한계는 역시 존재한다.

1. PDP는 변수들이 독립이라고 가정한다.
   앞서 수식에서 살펴보았듯이 PDP는 변수들이 독립이라고 가정하는데, 이는 실제 데이터에서는 현실적으로 불가능한 일이다. 실제 데이터셋을 구성하는 변수들은 각각 다른 변수들과 어느정도의 상관관계를 갖고 있기 때문에 이 데이터에선 PDP의 해석이 크게 유의미하지 않을 수도 있다. 그 이유는 상관관계가 존재한다면 변수들이 target에 미치는 영향은 매우 복합적일 수 있는데, PDP처럼 그저 한 변수와 target 변수와의 관계를 해석하여 결론을 내는 것은 다소 성급한 결론이라고 볼 수 있을 것이다.
2. Global한 해석은 가능하지만 local한 해석은 불가능하다.
   Partial dependence function을 계산할 때, marginal effect를 평균내어 계산하였다. 따라서 PDP는 데이터를 gloabal(전체적)으로 해석하는 것에는 용이하나, 개별 데이터 해석을 하는 것은 힘들다. 또한 평균을 냄으로써 가져오는 단점이 있다. 만약 어떤 데이터셋에서 절반정도가 변수 A가 양수값을, 나머지 절반의 변수 A가 음수값을 가지면 partial dependence function은 0에 수렴하는 값을 가진다. 이 경우 target변수와의 관계성을 해석하는데 어려움이 생긴다.(아무런 관계성도 발견할 수 없기 때문)
3. PDP는 변수의 분포를 보여주지 않는다.
   PDP는 변수의 분포도는 제공하지 않는데, 변수의 분포를 모른 채 PDP 해석을 진행하게 되면 잘못된 해석을 할 여지가 있다. 이는 PDP 패키지가 아닌 따로 분포도를 그려봄으로써 해결할 수 있다.

---

오늘은 Interpretable Machine-learning의 기본인 Partial Dependence Plot에 대해 공부해보았다. 다음 포스팅에서는 머신러닝 해석에 사용되는 모델 중 하나인 LIME에 대해 다뤄보도록 하겠다! 포스팅에서 사용한 코드는 여기를 참고하면 된다!

참고문헌
https://christophm.github.io/interpretable-ml-book/pdp.html
https://scikit-learn.org/stable/modules/generated/sklearn.inspection.plot_partial_dependence.html