[Theory] 손실함수(Loss function)의 통계적 분석

오늘은 머신러닝/딥러닝의 기본기를 다시 한 번 다지기 위해 손실함수(Loss function) 에 대해 낱낱이 다루는 내용을 준비했습니다.

0. 들어가며

지금까지 머신러닝, 딥러닝 모델 코드를 짤 때 성능 평가를 위해 분류면 categorical crossentropy, accuracy를 써야지~ 회귀면 MSE 써야지~ 하고 별 다른 생각 없이 손실함수를 쓴 경우가 종종 있습니다. 머신러닝과 딥러닝의 가장 기본이면서 중요한 개념인 손실함수의 개념, 손실함수 최소화 원리에 대해 정확히 이해하기 위해 본 포스팅에서 다뤄보고자 합니다.

1. 손실함수(Loss Function) 란?

머신러닝/딥러닝 모델을 이용해 target을 예측할 때 우리는 성능평가라는 것을 합니다. 이는 예측값이 실제 값을 얼만큼 정확히 예측했는지를 평가하는 과정입니다. 손실함수는 실제 값과 예측 값의 차이를 측정하는 측도입니다. 만약 실제 값과 예측 값이 차이가 크다면 오차가 크다고 말하는데, 이 오차가 커지면 손실함수 값은 커지가 됩니다. 즉, 손실함수를 최소화하는 적절한 모델을 찾는 것이 머신러닝/딥러닝의 목표인 것이죠!

이렇게 손실함수는 모델 최적화를 위해 반드시 사용되어야 하는 성능평가 함수입니다. 이제 손실함수에는 어떤 종류가 있는지, 손실함수 최소화는 어떻게 이루어지는지에 대해 살펴보겠습니다.

2-1. 회귀(Regression) 손실함수

회귀분석(Regression analysis)는 연속형 target 값을 예측하는 분석 기법을 말합니다. 회귀분석에서 가장 유명하고, 많이 사용되는 손실함수는 바로 MSE(Mean Squared Error) 입니다. 회귀분석 상황을 아래와 같이 정의해봅시다.

• $y_i$: $i$번째 실제 target 값 $(i = 1, 2, \dots, n)$
• $\hat{f}(x_i)$: i번째 설명변수 $x_i$와 적합한 모델 $\hat{f}$를 이용해 예측한 값

그러면 MSE는 다음과 같이 정의됩니다.
$ MSE = \frac{1}{n}\sum_{i=1}^{n}(y-\hat{f}(x_i))^2$

즉, MSE는 실제값과 예측값의 차이인 오차의 제곱합의 평균입니다. 회귀분석에서는 MSE를 최소화하는 함수 $ \hat{f} $를 찾는 것이 목표입니다. 이렇게 MSE는 매우 직관적이고 이해하기 쉬운 손실함수입니다. 이런 MSE에도 치명적인 단점이 있습니다.

1. 아래 그림과 같이 한 점에서의 오차가 매우 큰 경우, 이 큰 오차의 제곱이 MSE에 반영되기 때문에 MSE 또한 매우 커져 MSE가 inflation 되는 현상이 발생할 수 있습니다.
   
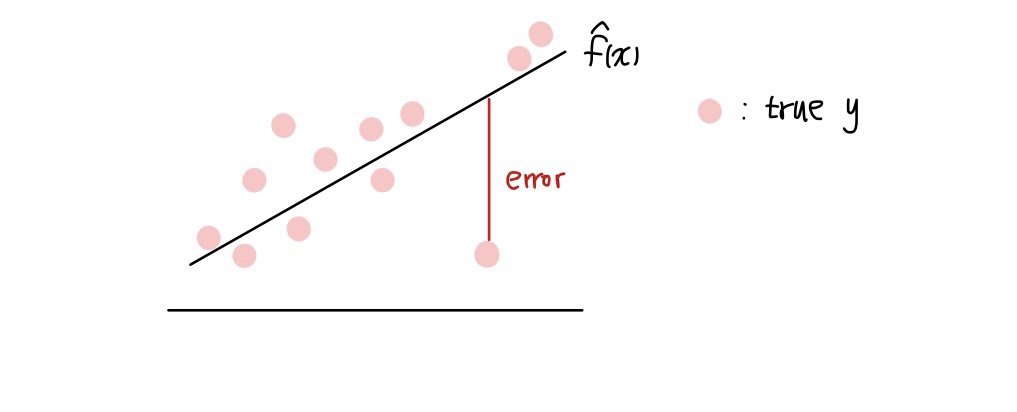
2. Target 값의 scale에 따라 MSE 크기가 달라질 수 있습니다. 예를 들어 target이 달러 단위이면 오차 단위는 $1 이지만, 원 단위이면 오차 단위는 1000으로 늘어납니다. 이를 해결하기 위해 회귀에서는 MSE보다 MSE에 루트를 씌운 RMSE라는 손실함수를 사용하기도 합니다.

회귀분석에서 사용하는 또다른 대표적인 손실함수 중 하나는 MAE 입니다.
$ MAE = \frac{1}{n}\sum_{i=1}^{n}|y_i - \hat{f}(x_i)|$ MAE는 MSE와 달리 오차의 절댓값의 평균을 손실함수로 사용합니다.

2-2. 분류(Classification) 손실함수

분류에서의 손실함수는 크게 두 가지로 나뉩니다. 첫번째 경우는 분류 클래스가 두 개인 경우이고, 두번째 경우는 분류 클래스의 수가 두 개 이상인 경우입니다.

분류에서의 손실함수를 최소화 할 때는 가능도 함수(Likelihood function) 이라는 개념이 사용됩니다.

1. 이항분류(Binarry Classification)

이항분류는 말 그대로 target 값이 두 개의 클래스 중 하나를 갖는 것을 말합니다. 대표적으로는 target이 0 혹은 1 을 갖는 케이스가 바로 이항분류 케이스입니다. 이항분류의 손실함수는 베르누이분포에서 착안합니다.

베르누이분포는 성공 혹은 실패인 시행을 1, 0으로 나타내는 베르누이 확률변수가 따르는 분포입니다. 이 때 성공 확률을 $p$ 라 하고 독립인 베르누이 시행을 $ n$ 번 시행했을 때의 결합확률질량함수는 다음과 같습니다. (각 독립적인 시행을 $ x_i$ 라 하겠습니다.) \

$ f(x_1, x_2, \dots, x_n;p) = p^{\sum_{i=1}^{n}x_i}(1-p)^{n-\sum_{i=1}^{n}x_i}$

가능도함수의 정의에 의해, 이 상황에서의 가능도 함수는 다음과 같습니다. \

$ L(p) = p^{\sum_{i=1}^{n}x_i}(1-p)^{n-\sum_{i=1}^{n}x_i}$

가능도함수를 최대로 만드는 모수 (p ) 를 찾기 위해서는 로그가능도함수를 먼저 찾습니다.\

$ \ell(p) = log(p)\sum_{i=1}^{n}x_i + log(1-p)(n-\sum_{i=1}^{n}x_i)$

이 로그가능도함수를 최대화 하는 모수 $p$ 가 바로 가능도함수를 최대화하는 모수입니다.

이제 다시 이항분류의 손실함수로 돌아오면, 이항분류에서의 손실함수는 아래와 같습니다. \

$ \ell(p) = -\sum_{i=1}^{n}[y_i log(p_i) + (1-y_i)log(1-p_i)]$

이를 자세히 보면 앞서 다룬 베르누이분포의 로그가능도함수 그 형태가 부호를 제외하고 같습니다. 이항분류에서는 손실함수를 최소화하는 것이 목표인데, 이항분류에서의 손실함수를 최소화하는 $ p $는 곧 베르누의분포의 로그가능도함수를 최대화하는 $p$ 라는 것을 알 수 있습니다.

우리는 이 손실함수 $ \ell(p) = -\sum_{i=1}^{n}[y_i log(p_i) + (1-y_i)log(1-p_i)] $ 를 binary crossentropy 라고 합니다.

2. 다항분류(Multi Classification)

이제 target에서의 클래스가 세 개 이상인 다항분류 케이스에 대해 살펴보겠습니다. 이항분류는 베르누이분포와 유사했었는데, 비슷한 아이디어로 다항분류는 다항분포와 유사할 것이라고 추측할 수 있습니다. 이 추측이 맞는지 알아봅시다!

다항분포는 결과값이 세 개 이상인 것으로, 각 결과가 특정한 횟수만큼 나타낼 확률을 기반으로 하는 확률분포입니다. 클래스 $ 1, 2, \dots, k $ 가 나올 확률을 각각 $ p_1, p_2, \dots, p_k $ 라 합시다. 그리고 각 클래스가 나오는 횟수를 $ x_1, x_2, \dots, x_k $ 라 하면 다항분포의 확률질량함수는 다음과 같이 나타낼 수 있습니다. 이 때 총 시행 횟수를 $ n $ 이라 합니다.
$ f(p_1, \dots, p_k) = \frac{n}{x_1 ! x_2 ! \dots x_k !} p_1^{x_1}p_2^{x_2}\cdots p_k^{x_k}$

이제 앞서 이항분류처럼 다항분포의 로그가능도함수를 구하면 다음과 같습니다.
$ \ell(p_1, \dots, p_k) = x_1 log(p_1) + x_2 log(p_2) + \cdots + x_k log(p_k) = \
\sum_{i=1}^{n}\sum_{j=1}^{k}x_{ij}log(p_{ij})$

다항분류에서의 손실함수는 $ -\sum_{i=1}^{n}\sum_{j=1}^{k}x_{ij}log(p_{ij})$ 로, 이를 category crossentropy 라 합니다.
따라서 다항분류의 손실함수를 최소화하는 $p_{ij}$ 는 곧 다항분포의 로그우도함수를 최대화하는 $p_{ij}$ 입니다.

정리하면, 분류에서의 손실함수는 이항분포, 다항분포의 로그가능도함수와 밀접한 연관이 있습니다. 손실함수를 최소화하는 모수는 곧 로그가능도함수를 최대화하는 모수입니다.

---

이렇게 회귀, 분류에서의 손실함수와 이와 연관된 통계적 개념들을 살펴보았습니다. 손실함수는 머신러닝, 딥러닝의 기본이기 때문에 이런 통계적 기본 개념을 다시 한번 상기하는 것도 중요하다고 생각합니다!

오늘의 손실함수 포스팅은 여기까지 마치겠습니다 :)